弦楽器にとって振動モードと剛体としての運動条件が響きをきめる重要な要素になっています。
皆さんがご存じなように一次振動モードはわかりやすいですね。
ちなみに今日ではギターやベースなどの弦楽器の演奏をiPhoneで撮影すると、カメラに搭載された CMOSイメージセンサの誤差によって起こる “ローリングシャッター現象” によってまるで自分の目がオシロスコープになったかのような映像で見ることができます。
ローリングシャッター現象とは CMOSセンサーが目の前の風景を一度に全て記録せずにイメージの上部から順番に記録を行なうために、高速に動く被写体を撮影すると取り込む時差によよって歪みが生じておこる現象です。
一次元モードのアニメーション
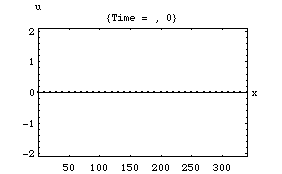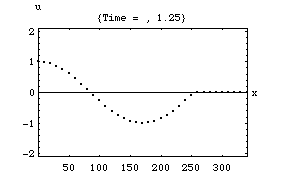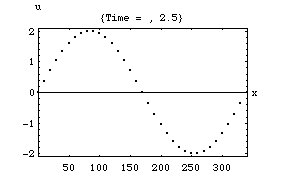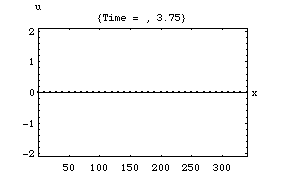
粒子速度
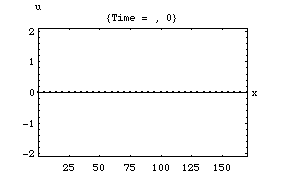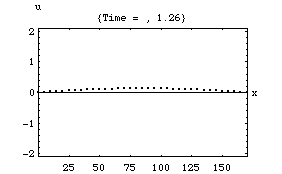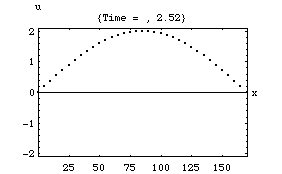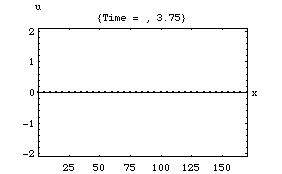
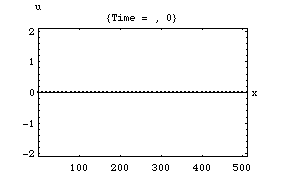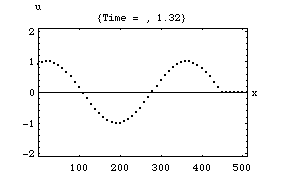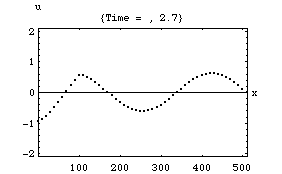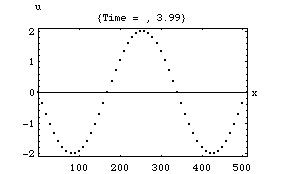
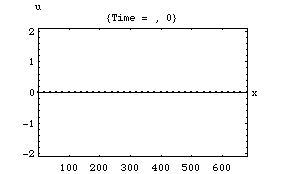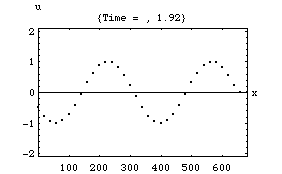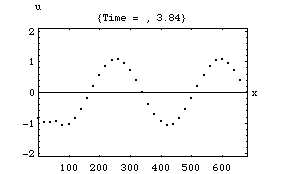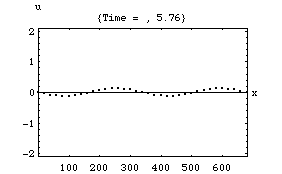
以下の4つのアニメーションは、それぞれ一次元音場の点 (0)において音が発生し、x方向へ伝搬し、右端の剛壁で反射、後退波が発生、その後両者の干渉によって定在波が発生する様子を示している。またこれは2次元音場における「軸波 (axial mode)」の一つの断面とみなすこともできる。
1.波の数が一つの時
2.波の数が二つの時
3.波の数が三つの時
4.波の数が四つの時
ニ次元モードのアニメーション
二次元音場の固有振動モードの生起
以下のアニメーションは剛壁に囲まれた二次元音場の点(0,0)において音が発生し、(x,y)両正方向へ伝搬し、剛壁で反射、後退波が発生、その後両者の干渉によって定在波が発生する様子を示す。またこれは3次元音場における「接線波 (Tangential Mode)」の一つの断面とみなすこともできる。
音圧
1.固有振動モード(1、1、0)
このアニメーションは、xy 平面における音圧 p の時々刻々の変化の様子をあらわしている。
剛壁に囲まれた二次元音場の点(0,0)において音が発生し、(x,y)両正方向へ伝搬し、剛壁で反射、後退波が発生、その後両者の干渉によって定在波が発生している。
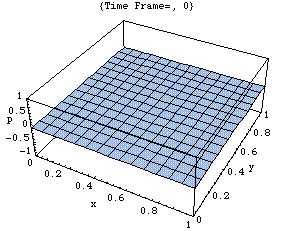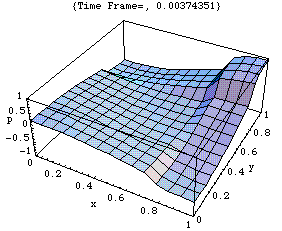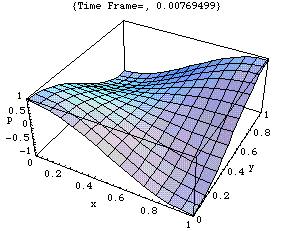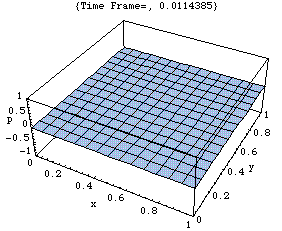
<注意>厳密には、二次元音場において点音源から生じた音は「円筒波」として伝搬すると考えられる(あるいは、二次元の波動方程式の解は円筒波を表わすハンケル関数を用いて得られる)。しかしここでは簡単のため、現象を平面波で近似して示している。このため波面は矩型となっている。なお数学的に球面波は平面波を重ね合せて得られることが知られている。
2.固有振動モード(1、2、0)
二次元モード
このアニメーションは、xy 平面における音圧 p の時々刻々の変化の様子をあらわしている。
剛壁に囲まれた二次元音場の点(0,0)において音が発生し、(x,y)両正方向へ伝搬し、剛壁で反射、後退波が発生、その後両者の干渉によって定在波が発生している。
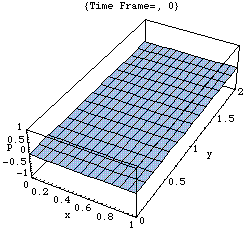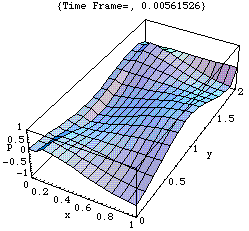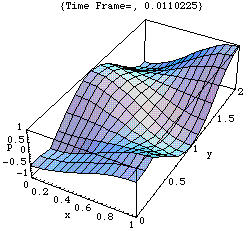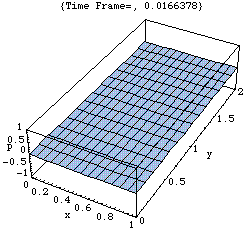
<注意>厳密には、二次元音場において点音源から生じた音は「円筒波」として伝搬すると考えられる(あるいは、二次元の波動方程式の解は円筒波を表わすハンケル関数を用いて得られる)。しかしここでは簡単のため、現象を平面波で近似して示している。このため波面は矩型となっている。なお数学的に球面波は平面波を重ね合せて得られることが知られている。
粒子速度
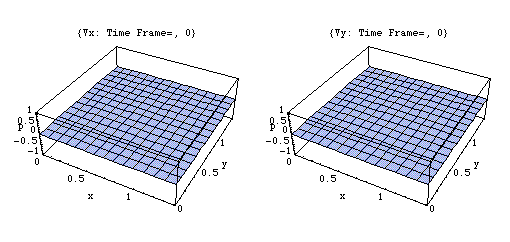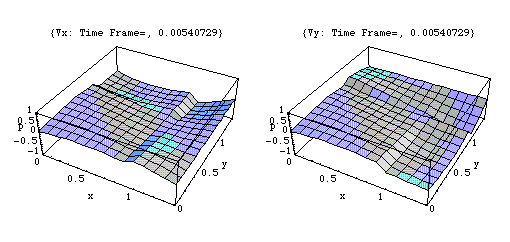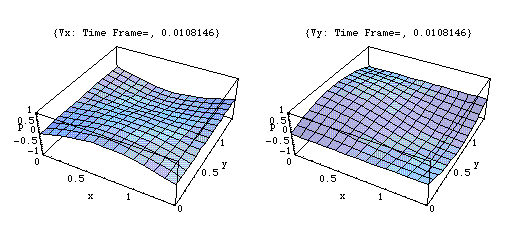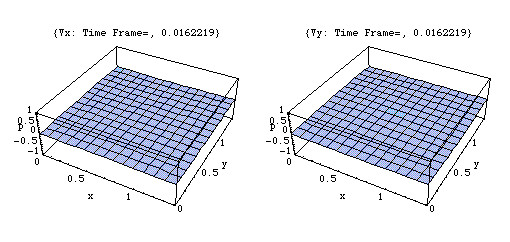
上の(1,1,0)の場合の、x, y 二つの方向に関する粒子速度成分を左右の図で示す。反射波が干渉した結果、剛壁における法線方向速度成分が0になる様子が示されている。
固有振動モード(1、1、0)
このアニメーションは、xy 平面における粒子速度 u の時々刻々の変化の様子を x , y 二つの方向に分けて表わしている。
剛壁に囲まれた二次元音場の点(0,0)において音が発生し、(x,y)両正方向へ伝搬し、剛壁で反射、後退波が発生、その後両者の干渉によって定在波が発生している。
<注意>厳密には、二次元音場において点音源から生じた音は「円筒波」として伝搬すると考えられる(あるいは、二次元の波動方程式の解は円筒波を表わすハンケル関数を用いて得られる)。しかしここでは簡単のため、現象を平面波で近似して示している。このため波面は矩型となっている。なお数学的に球面波は平面波を重ね合せて得られることが知られている。
三次元モードのアニメーション
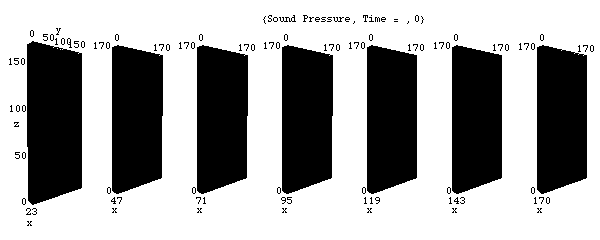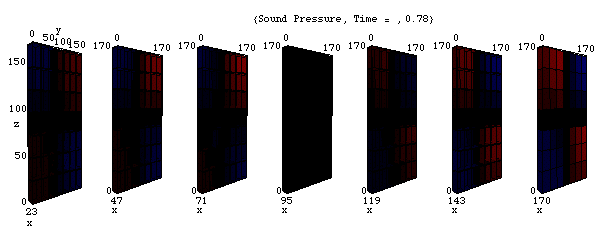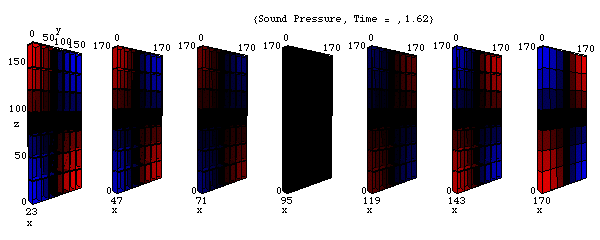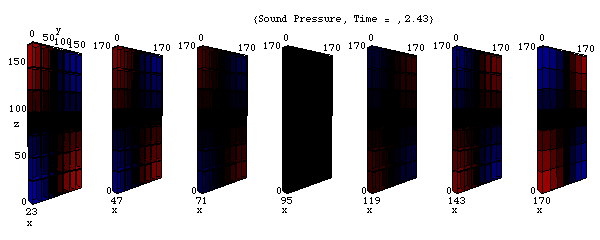
音圧の固有振動モード (1,1,1)
このアニメーションは、xyz 空間における音圧 p の時々刻々の変化の様子を表わしている。
剛壁に囲まれた三次元音場の点(0,0,0)において音が発生し、(x,y,z)それぞれの正方向へ伝搬し、剛壁で反射、後退波が発生、その後両者の干渉によって定在波が発生している。
( 三次元空間を表現するのは困難なため、三次元空間の断面を並べて表現している。)
![]()
ポテンシャルモード
ここでは速度ポテンシャルの変動を黒点の大きさの変化で示している。つまり、音圧の変動はその動きの逆(ポテンシャルが大きい場所では音圧は小)で示されている。室の中央部で音圧が低く周壁部で音圧が高いことが分かる(アニメーションでは、中央での黒丸の動きが大きく、ポテンシャルの変動が激しいことが表されている)。
このアニメーションは、立方体室の点(0,0,0) から音が発生し、時々刻々のポテンシャルの変化の様子を表わしている。
1331mo111
(1,1,1)モードです(776 k)(.mov)
