ピタゴラスが見出したことについての説明が短文でわかりやすく書かれているので共有させていただきました。

“ドレミファソラシド”を発明したのは誰か

2018年11月11日 11時15分 プレジデントオンライン

• 

■「音階」を発明したのは誰か？数学と音楽の関係をご紹介したい。

みなさんご存じの「ドレミファソラシド」の音階。実はこれを発明したのは、「ピタゴラスの定理」で有名な古代ギリシャのピタゴラスなのだ。ある日、散歩をしていたピタゴラスの耳のなかに、鍛冶職人がハンマーで金属を叩く「カーン、カーン」という音が入ってきた。そしてピタゴラスは、美しく響き合う音と、そうでない音があることに気づいた。不思議に思い、いろいろな種類のハンマーを叩いて調べたところ、美しく響き合うハンマーどうしは、それぞれの重さの間に単純な整数の比が成立することを発見したのだ。

特に2つのハンマーの重さの比が2：1の場合と、3：2の場合に、美しい響きになった。そこでピタゴラスと弟子たちはさらに熱心に音階の研究に取り組んだ。彼らは「モノコード」と呼ばれる、共鳴箱の上に弦を1本張った楽器を発明し、2台のモノコードを同時に弾いて、弦の長さを変えながら美しく響き合う位置を探した。その結果、やはり弦の長さが2：1になったときに2つの音が完全に溶け合い、3：2や4：3のときにも音が調和することがわかった。

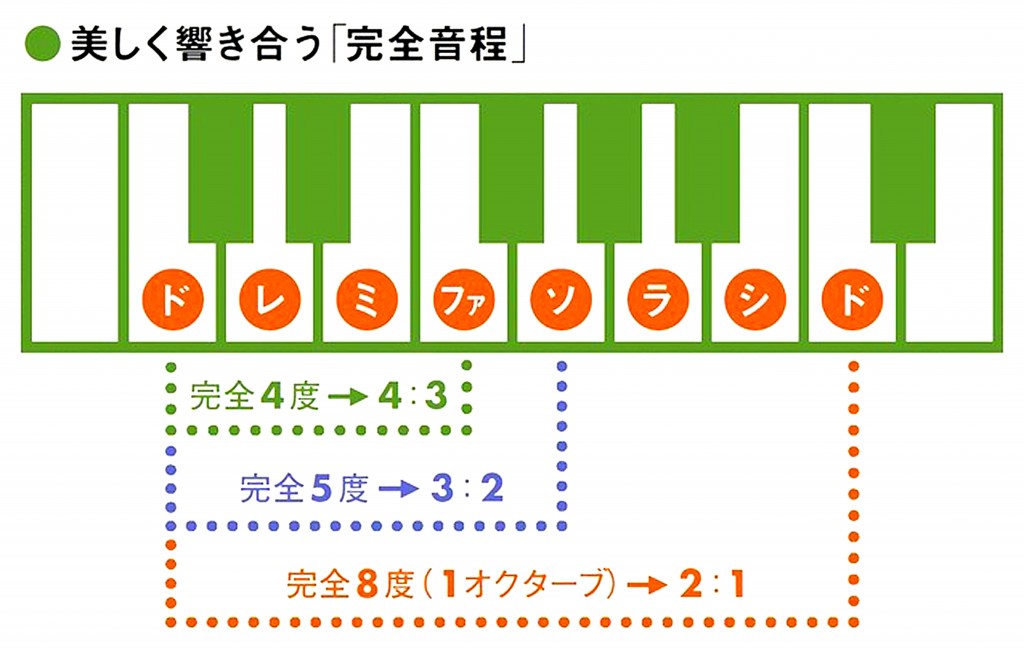
「ドレミファソラシド」の低いドから高いドまでの音程の幅を「1オクターブ」という。そして、その1オクターブ離れた2つの音は同時に響くと、高さの違う「同じ音」に感じられ、濁りなく美しく調和する。音楽では、音程（2つの音の、音の高さの差）を「度」で表す。同じ高さの音どうしは「1度」、ドとレのように隣り合う音は「2度」になる。特に美しく響き合う「完全音程」は1オクターブのなかに「完全4度」（ドとファ）、「完全5度」（ドとソ）、「完全8度」の3つがあって、弦の長さの比と関係は図のようになる。完全8度だけでなく、美しく響き合う音程になるときの2つの弦の長さの比が、簡単な整数の比になることを発見したピタゴラスたちは非常に感銘した。

数字とはかけ離れたものだと思われていた音楽の美しさがリンクしていたという事実。彼らはそこに何らかの神の意思をくみとり、数字はすべてのものとつながりがあるのではないかと考え、その後は「万物は数である」というスローガンを掲げて活動するようになった。ピタゴラスと弟子たちの熱心な啓蒙により、古代ギリシャの人々は、宇宙は数の調和でつくられていると考えるようになる。宇宙の調和の根本原理は「ムジカ」であり、その調和は「ハルモニア」である。英語でムジカは「ミュージック」、ハルモニアは「ハーモニー」だ。

こうして古代ギリシャ以降、中世に至るまで、音楽は哲学や科学に近く、秩序や調和の象徴としてとらえられていた。数学（mathematics）の語源はギリシャ語の「マテーマタ＝学ぶべきもの」で、古代ギリシャにおけるマテーマタ（数学＝学科）は、「算術（静なる数）」「音楽（動なる数）」「幾何学（静なる図形）」「天文学（動なる図形）」の4分野から成っていたのだ。古代ギリシャ人にとって音楽（美の中にある数）がいかに「学ぶべきこと」であったかが、うかがえるのではないだろうか。

———-永野裕之永野数学塾塾長1974年、東京都生まれ。東京大学理学部地球惑星物理学科卒。大人の数学塾・永野数学塾塾長。著書に『統計学のための数学教室』『ふたたびの高校数学』『東大→JAXA→人気数学塾塾長が書いた数に強くなる本 人生が変わる授業』など。———-（永野数学塾塾長 永野 裕之 構成＝田之上 信　写真＝iStock.com）