弦楽器のしくみは多少難解ですが‥「 オールド・ヴァイオリン 」と、「 “写し”として製作されたヴァイオリン 」、そして「 贋作ヴァイオリン 」を見分けるには、『 オールド弦楽器の製作方法 』を知ることが重要ではないかと 私は考えます。

そこで、16世紀中頃から 18世紀の終わりまで製作された弦楽器の音響システムを実証するために、2015年に私が製作したチェロの事例を用いて「オールド弦楽器」の特徴についてお話しさせていただこうと思います。

なお、ここでは ヴァイオリンより多少バランスの違いが見えやすいチェロを用いますが、基本的な仕組みはヴァイオリンや ビオラも同じとご理解ください。

Cello 1700年頃 パーツ無し重量 2280g / 総重量 2789g

弦楽器は固有振動がそのキャラクターを決定します。ですから製作する場合は まず、総重量とそれを構成する それぞれの部分の重量配置 ( 重心コントロール )と、 それらのゆれ方の関係性を決定する必要があります。

そこで まず基本からですが、 オールド・チェロは 響胴サイズが様々です。これを アントニオ・ストラディヴァリ ( ca.1644-1737 )や、ジロラモ・アマティ Ⅱ ( 1649-1740 )、ヨーゼフ・ガルネリ ( 1698-1744 ) などのチェロで見て下さい。

 

● Girolamo Amati Ⅱ ( 1649-1740 ) Cello, 1690年                                      F. 737 -352 – 243 – 439 / B. 738 – 352 – 239 – 431                                    Stop 397mm / ff ( between Tow holes ) 82.2mm                                     Head L. 209mm / Eyes width 63.2mm

● Antonio Stradivari ( ca.1644-1737 ) Cello,”Gore-Booth” 1710年     F. 756 – 343.5 – 230 – 437 / B. 756 – 341.5 – 229 – 437                            Stop 407mm / ff 90.8mm / Head L. 204.5mm / Eyes width 67.4mm

● Antonio Stradivari ( ca.1644-1737 ) Cello, “Pleeth” 1732年頃           F. 719 – 339.5 – 231 – 422 / B. 717 – 340 – 230 – 420                              Stop 398mm / ff 92.8mm / Head L. 214mm / Eyes width 66.5mm

● Antonio Stradivari ( ca.1644-1737 ) Cello, “Josefowitz” 1732年      F. 693.5 – 316.5 – 219 – 403 / B. 690 – 319.5 – 220 – 408                       Stop 375mm / ff 86.2mm / Head L. 204mm / Eyes width 67.5mm

● Guarneri del Gesù ( 1698-1744 ) Cello, “Messeas” 1731年                  F. 730 – 349 – 241 – 434 / B. 735 – 354 – 243 – 437                                  Stop 392mm / ff 102mm / Head L. 210mm / Eyes width 66.0mm

このように オールド・チェロは、総重量の前提となる響胴の大きさを理解するだけでも 難易度は高いと思います。

それらを勘案した上で、音響システムの実証用チェロ製作時に私が直接的に参考としたのは冒頭の画像のものも含めた下記の5台でした。

Nicola Albani / Cello ( Worked at Mantua and Milan 1753-1776 )

① Cello 1700年頃 　　　　　　　　　　　　　　　　　　　   パーツ無し重量 2280g ( Back 735 – 349 – 225 – 430 / Stop 403.0 )　総重量 2789g

② Nicola Albani Cello ( Worked at Mantua & Milan 1753～1776 )パーツ無し重量 2250g ( Back 734 – 343 – 236- 427.5 / Stop 392.5 )総重量 2747.8g

③ Giovanni Battista Guadagnini ( 1711-1786 ) Cello 1757年 　　  総重量 2584g ( Back 712.2 – 332.7 – 237 – 419 / Stop 391.1 )

④ Giovanni Battista Guadagnini ( 1711-1786 ) Cello 1743年頃 　  総重量 2456g ( Back 716.6 – 340 – 228.7 – 423.3 / Stop 391.0 )

⑤ Cello 1790年頃 　　　　　　　　　　　　　　　　　　　　パーツ無し重量 1826g ( Back 707 – 320 – 215 – 408 / Stop 379 ) 　 総重量 2330g

そして、最終的に私は下記の規格を採用しました。

● Joseph Naomi Yokota Cello, 2015年                                                             総重量 2389g

表板サイズ：745.5 – 347.0 – 243.0 – 449.0                                                      裏板サイズ：741.0 – 356.5 – 239.5 – 448.0                                                      側板：ネック側 108.3mm – エンドピン側 120.0mm

表板アーチ：28.7mm                                                                                                     裏板アーチ：31.8mm

ヘッド長：205.0mm（ ボトム・ヒール位置まで ）                                スクロール・アイ幅：66.2mm 指板：30.0mm – 62.4mm – 583.5mm ストップ：403.0mm

この実証用チェロで重要と考えたのは次の5点です。

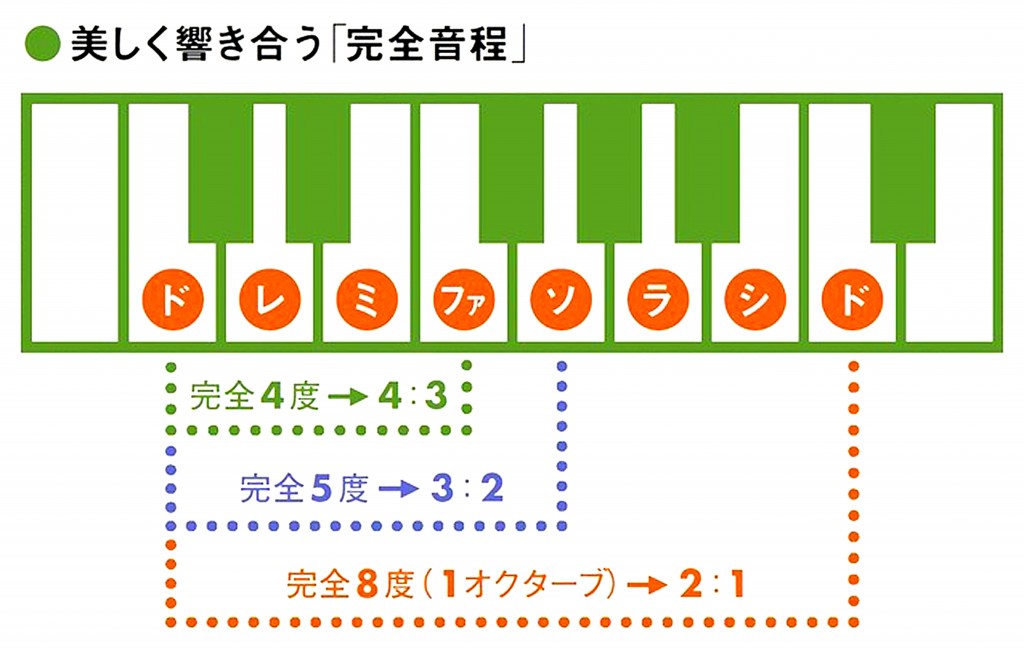
① オールド弦楽器の豊かな響きは それぞれの部分の振動が合成されることで成り立っていると考えられます。そして、それは 振動体の質量や長さが整数倍の関係のときに重なりやすいと推測できます。

例えば、下図のチェロのように 指板も含めたネック部と 響胴の重さの関係は 1 : 3 で、ヴァイオリンのそれは 1 : 2 といった設定が望ましいと私は考えます。

また、現代型の指板の場合は 指板が空中に突きでるネック端部に重心を合わせて 1 : 1 にしておくと 音量バランスが整いやすく、そのうえ指板自体の軸組を工夫することで運動特性をある程度 選択できるため、響胴に対してのバランスをあわせるときの大事な選択条件であると思われます。

② 弦楽器で深い響きを生むためには駆動系と変換点のエネルギーロスを減らすこと‥ あえて極端な表現をすれば「 振動の持続時間をすこしでも長くすること。」が大切だと考えられます。

このためには”対” となってゆれが残りやすい天秤の「 腹 – 節 – 腹 」の関係を剛性や運動を勘案し設定すること、そして振動エネルギーが通過する経路の工夫、変換点の「 節 – 腹 」の設定も表板の材料特性をよく観察し適切におこなうことで達成できると信じます。

③ 響胴部のバランスは6本の柱 ( ブロック ) の形状と、1本の交換式柱 ( 魂柱 ) やパフリング外縁部の剛性 ( 形状 ) を工夫して 表板と側板の接着面（ Reference plane ）に対しての重心位置をあわせることで調和させることが可能と思われます。

④ 響胴中央軸に対してのネック上面の軸は低音側 ( バスバー方向 )に合わせ、ネック下方面 の軸は裏板ジョイント方向にむけて「 ねじり 」を積極的に活用する設定で製作します。

⑤ 低音の共鳴現象が生じやすいように 表板の重さはバスバー無しの白木状態で 350g以下で、裏板は 550g以下、側板部が 500g以下とし、響胴部のなかで 表板と裏板側 ( 側板を含む )の関係を 1 : 3 で製作します。

同じく響胴とネック部の関係を 1 : 3 とするために指板は 200g以下で ネック & ヘッドは 300g以下にします。これらの合計である 2000g以下にするためには、立体的形状や幾何剛性を積極的に利用し安定した状態が持続できるように工夫します。

干渉についてのメモ

■ 自作チェロの重量配分図（ 塗装前 ）

総重量：2389.2g ( 完成日 2015-12-26 ) パーツ無し重量：1942.0g ( 白木 1885.5g ) / パーツ合計：447.2g

重量配分 ネック部 485.5g ： 響胴 1456.5g

塗装前ネック & ヘッド：297.0g – 指板 & ナット：186.0g                   表板部： 411.0g – 側板部：484.7g – 裏板部：531.0g

このチェロは 仕上がり総重量が 2389.2g でしたが、これはもちろん偶々ではなく着手時の目標値が 2250g ～ 2500g でしたので計算の通りといったところです。

現代では チェロの重さは 2300g～3200g 位で、個体差が大きいようです。なお、一般的に使用されているパーツ重量の合計は 380g～580g 程で、普及品タイプのチェロはパーツ無し( 指板含む )重量が 2400g～2800g ほどだと思われます。

あくまで個人的な意見ですが‥ 私は チェロの総重量が 2900g を越えるのは避けたほうが望ましいと思っています。例えば、2012年製 GLIGA gemsⅠシリーズの 初心者用チェロは パーツ無し重量が 2800gで、総重量が 3186g もありました。

GLIGA Cello ( gems Ⅰ), 2012年

こういう楽器は響胴からネック、ヘッドが一直線に硬直していて鳴らすとチューニングも狂いやすく、響胴も硬いのでボーイングが難しく 右手が疲れやすいのではないでしょうか。

その上、音量が望めませんので 合奏楽器としては薦められません。こういう現実を常々目にしていますので、私は 初心者用のチェロがもっと楽器として性能が改善されることを心から願っています。

■ 響胴の軸組

私は 18世紀末までの弦楽器製作者は 響胴の「 節と腹 」の原理をほぼ正確に理解し、実際に用いていたと考えています。

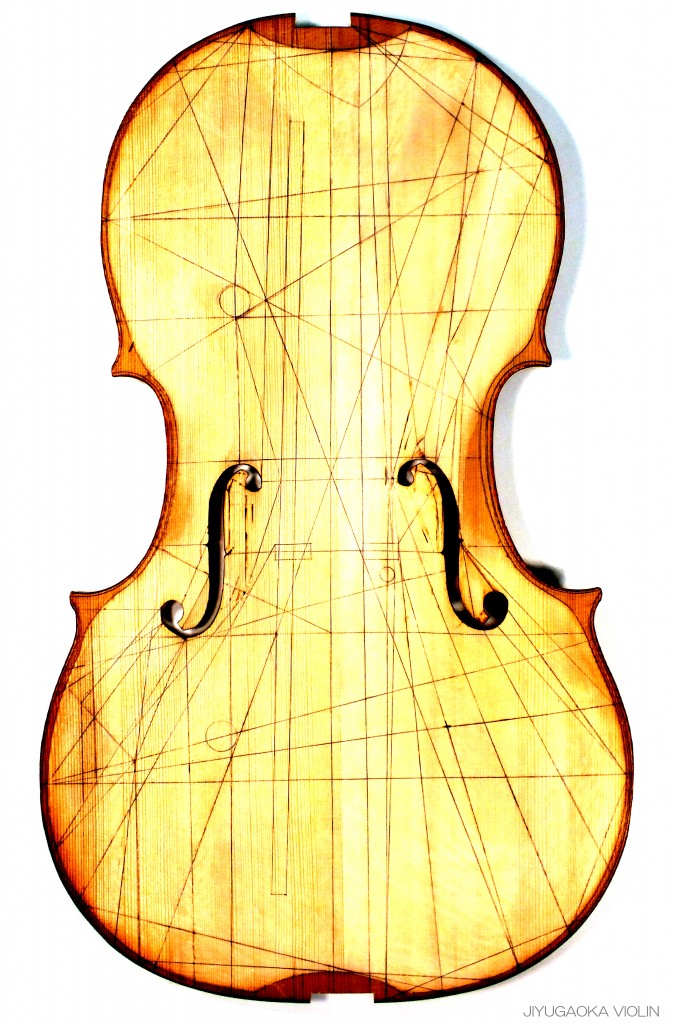
それらの要素をバランスよく組み合わせるためには 座標となる多数の軸線が必要と考えられます。

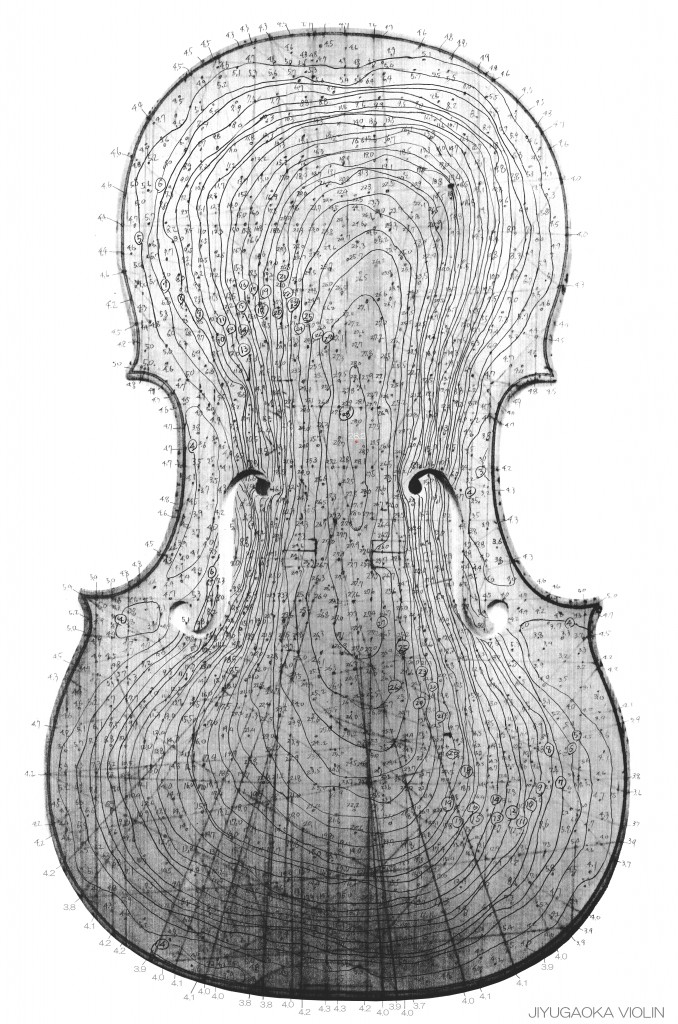
このため、私は 16世紀中頃から 18世紀の終わりまで製作された弦楽器の音響システムとしてこれらに残されている座標軸線の痕跡を検証し、表板や 裏板の軸線としてまとめてみました。

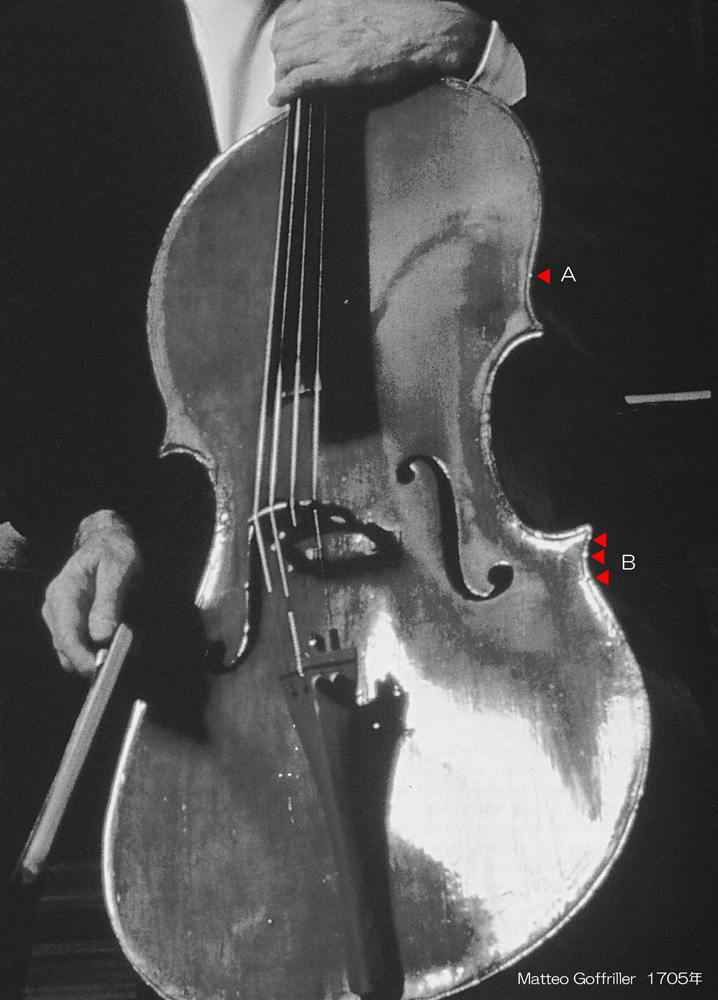
ヤーノシュ・シュタルケル（János Starker 1924 – 2013 ）さんが使用していたチェロは、1705年にベネチアで Matteo Goffriller ( 1659–1742 ) が 製作したものとされています。

 

この部分の’傷’は ストラディヴァリ・ソサエティの エドゥアルド・ウルフソン（ Eduard Wulfson ）氏が所有し、ナターリャ・グートマン（ Natalia Gutman ）さんが使用している グァルネリ・デル・ジェスが製作したとされる 1731年製のチェロとも共通しています。

• 

• 

Bartolomeo Giuseppe Guarneri ( 1698-1744 )                           Violoncello 1731, ” Natalia Gutman ”

このガルネリが製作したチェロは A ゾーンと B ゾーンの’傷’がとくに深くつけられています。

1982年にニューヨークで生まれたチェリスト、アリサ・ワイラースタイン（ Alisa Weilerstein ）さんが 2014年から使用しているチェロにも同じ特徴があります。

この楽器は Domenico Montagnana が 1730年に製作したとされています。そして この楽器ではA ゾーンとB ゾーンの傷が 確認できるとともに、C ゾーンの ‘深い傷’ も見ることができます。

私は これらを ‘節’としての ‘折れ軸’を調整した痕跡と考えています。

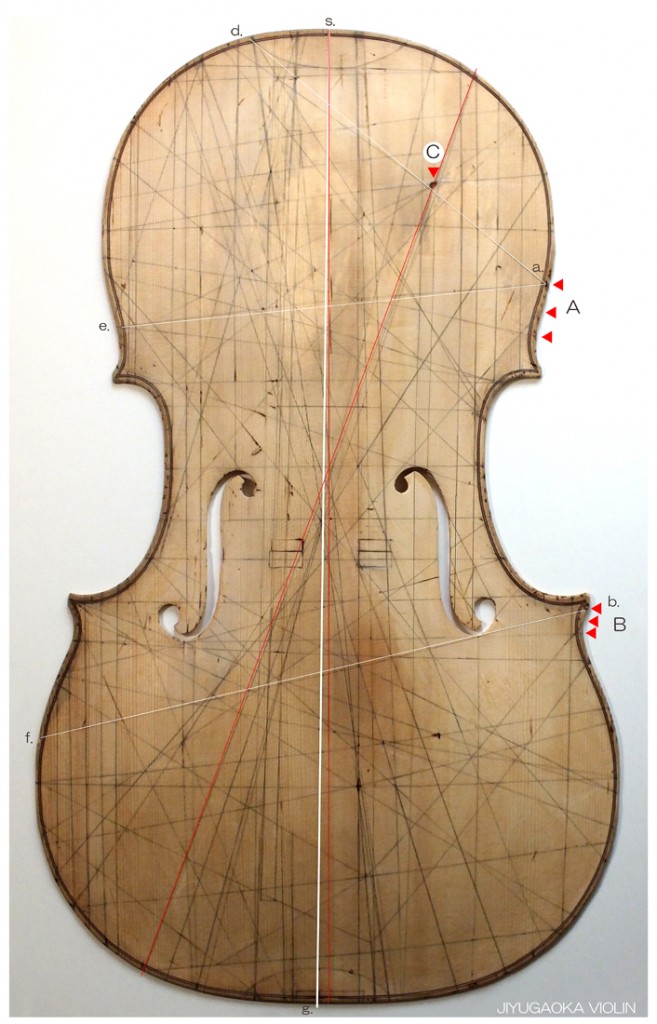
私は このような「オールド・チェロ 」などの分析から ‘座標’や ‘折れ軸’としてこれらの線分を製作のために 表板で 100本、裏板は 60本選び設定することにしました。

因みに、軸線が機能していない状態は 壊れた弦楽器で見ることが出来ます。

例えばこれは、壊れたコントラバスの修理をシュミレーションするために写真にしてプリントし切り抜いたあとで 破損個所をカットし表板の変形を実際のように折り込んだものです。

私の所見では‥ この破損の主因は、左右方向の剛性につながるアッパーやロワーの軸の不全です。

• 

• 

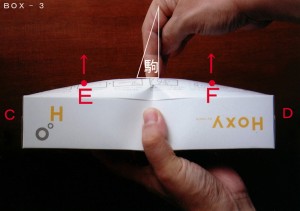
そもそも、弦楽器の多くは上図 点C, 点Dに弦の張力をかけることで 点A, 点B が 中央部に向かって倒れ込むような応力がかかるようになっています。

• 

• 

そして 点A, 点B からの応力は駒などによる中央部の剛性が高いゾーンを避けるように 点E と 点F のアッパーとロワー側にむかいます。

これによって弦楽器の多くは響胴にかかる応力で壊れないようになっています。

ですから、例として挙げさせていただいたコントラバスは下図のように折れ軸が機能するように、バスバーの形状を変更することでバランスを合わせ 再び使用出来るようにしました。

 

 

Nicola Gagliano ( ca.1710-1787 ) Violin, Napoli 1737年

「オールド・バイオリン」などでは 摩耗したように加工する “パティーナ加工 ( antique patina) ” が施されているものが多いので、ヘッド部を観察するときも これを念頭に置く必要があります。

その参考例として、このスクロールの右側突起部に注目してください。この部分は 製作された後の “修復” によって 現在この状態となっていると私は判断しました。

  　　　　　　　　　　　   　　

Nicola Gagliano ( ca.1710-1787 ) Violin, Napoli 1737年

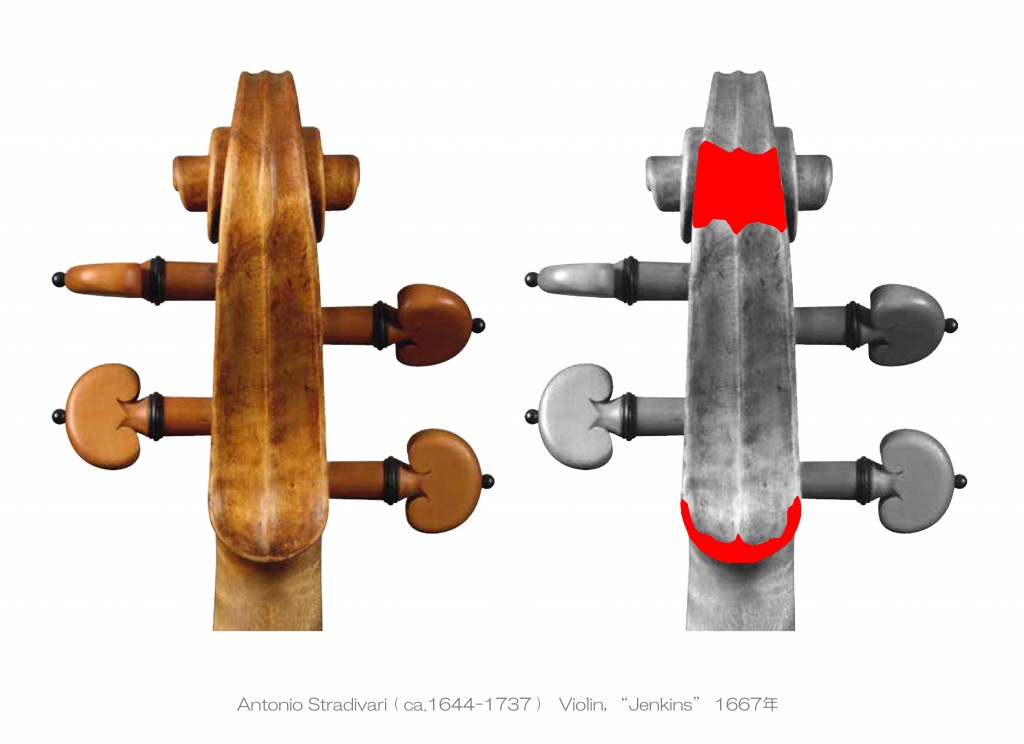
それは、この ヴァイオリン・ヘッドの “修理部分”が、同時期に製作されたヴァイオリンの摩耗痕跡（ 上中央 ）と 同様であったと考えられることが決め手となりました。

このような”特殊”と呼んでよいレベルの “パティーナ加工” が施されているヴァイオリンが複数台あるということは本当に素晴らしいと思います。

Nicola Gagliano ( ca.1710-1787 ) Violin, Napoli    1737年

　　　

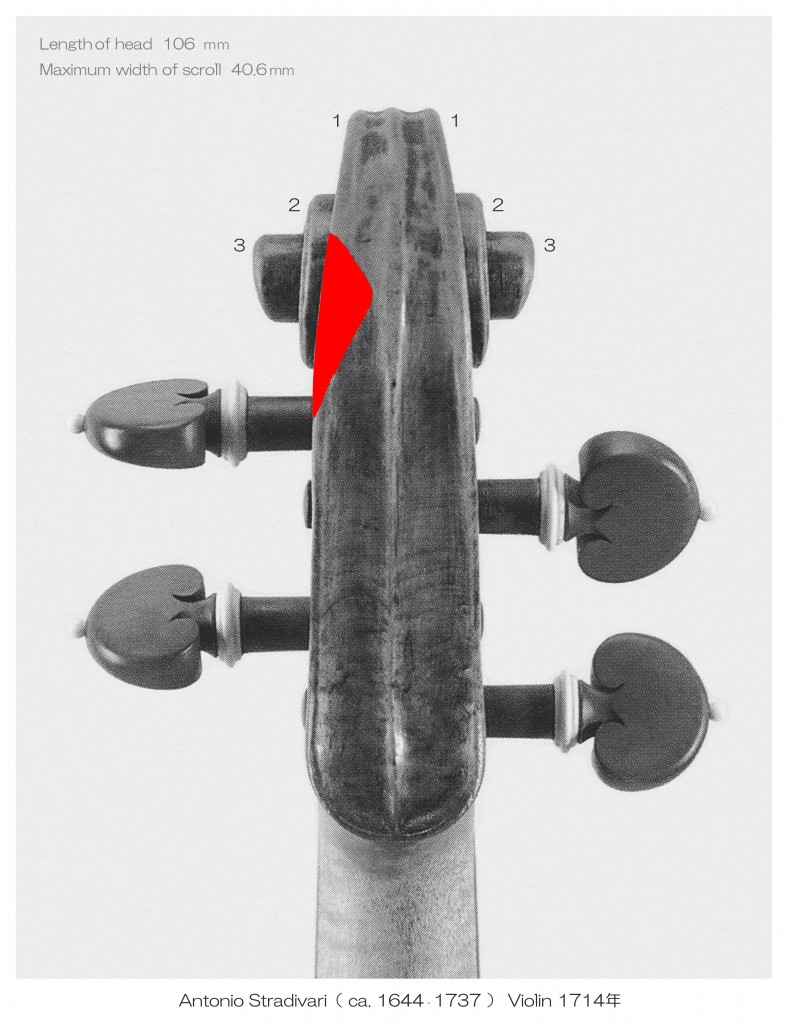
私は これらを、製作時に摩耗したような加工をする弦楽器製作者がいた状況証拠であると考えています。

Johann Jais Viola Tölz ( 1715-1765 ) Viola 1760年頃

また、上記のように 摩耗仕様で生み出された非対称性については、このビオラのように 着手時の設定段階（ 木取り ）で意図されたことが分る弦楽器との比較がその理解をより深めることに役立つと思います。

このように、摩耗痕跡タイプの “パティーナ加工 ” は 複数の作品で比較してみると 一定の法則性を見出すことができます。

Antonio Stradivari ( ca.1644-1737 )  Violin, Cremona “Lipinski” “Giuseppe Tartini”    1715年

たとえば このヴァイオリンは、1700年代に ヴァイオリンソナタ『 悪魔のトリル ( Devil’s Trill Sonata ) 』で有名となった 作曲家 ジュゼッペ・タルティーニ（ 1692-1770 ）が使用したとされる ストラディバリウスです。

 

私は 「 クレセント・カット（ Crescent cut ）」と呼んでいますが 三日月型の” 激しい摩耗痕跡 “があります。           

因みに、上写真右側の ” Cremonese ” も イタリア・クレモナに展示されている 有名なヴァイオリンです。このヴァイオリンの 該当する部分には 修復痕跡 が認められます。

さて、これは どう考えるべきでしょうか？

残念ながら このような摩耗痕跡を 『 演奏するためのチューニングなどですり減った。』 と思っている方も多いようで、実際にその判断の誤りにより このように ‘修復’ されてしまう弦楽器もあとを絶ちません。

これは、 ストラディヴァリが製作した装飾文様入りの有名なヴァイオリン “Sunrise” です。 彼が初期に製作した作品ですが 装飾加工も含めて製作時の状況がよく保存されていることでも知られています。

このヴァイオリン・ヘッドにも 小さなクレセント・カットが入っています。ところがその周りには他に摩耗したような痕跡はあまり見られません。

私は このヘッドにみられる摩耗部とその隣接部との ‘様子の違い’ を不自然（ = 意図的 ）であると感じます。

それから、これは オーストリア国立銀行が ウィーン・フィル（ Wiener Philharmoniker ）のコンサートマスターに貸与している 1709製ストラディヴァリウス ”ex Hämmerle” の ヘッド写真です。

2008年に定年退団するまで ウェルナー・ヒンク氏 ( Werner Hink 1943 – ) が使用し、その後 1992年から コンサートマスターに就任していた ライナー・ホーネック氏 ( Rainer Honeck 1961- ) が 演奏に用いている有名な楽器です。

クレセント・カットとなっていたと考えられる 赤色部は接木されているようですが、このヴァイオリンで摩耗部とその周りとの 『 様子の違い 』を 見て下さい。

下画像のように 私はスクロール部を 1段目、2段目、３段目と区別していますが、摩耗痕跡が 1段目のエッジ部でみとめられるのに 2段目、３段目のエッジ部は 完成時のままであるかのように フレッシュです。

この 1709製 ストラディヴァリウス ”ex Hämmerle” の ヘッド１段目とそれ以外のエッジ摩耗の差は、ほかの ストラディヴァリウス‥ たとえば 下写真の 1714年製でも 見ることができます。

この 1714年製のストラディヴァリウスでも、前出の1709年製のヘッド程ではありませんが 同じように三角形の接木がしてあるようです。また、摩耗痕跡も 1段目のエッジ部でみとめられるのに 2段目、３段目のエッジ部は 完成時のままであるかのように フレッシュです。

ヴァイオリンを演奏したことがある方でしたらイメージ出来ると思います。もし チューニングでヘッドに触れたことが摩耗の原因だとしたら 「 この景色 」はあり得ないのではないでしょうか。

これらを検証した結果、ストラディヴァリは 摩耗加工を 多少不自然になるのを承知のうえで、 音響上必要とおもわれる最低限にとどめた弦楽器製作者だと私は考えるようになりました。

さて‥ ヴァイオリン族のなかでも ヴァイオリンと ビオラは 演奏者がヘッドに触れることがある訳ですが、チェロのヘッドは人が触れることは殆どありません。

ところがオールド・チェロの中には、製作者が 前出の ストラディヴァリウスのヘッドと同じように 2、3段目はそのままで1段目だけを”激しく摩耗させた” チェロが存在します。

私も 最初にプロのオーケストラで 2プルトに座っているチェリストから 『 演奏の最中に目の前のオールド・チェロのヘッドをいつも眺めていてね‥ヘッドが ”激しくすり減った” 理由が何度考えてもまったく解からないんだけどどうして？』と質問された時には まったく説明できませんでした。

しかし、同じような質問を何人かから受けましたので 本腰をいれて調べることになりました。

これは 1997年に ヴェネチアの南西80㎞程の街 Lendinara で開催された展示会カタログ ” Domenico Montagnana – Lauter in Venetia ” Carlson Cacciatori Neumann & C. の 109ページに掲載されている 1742年に Domenico Montagnana が製作したとされるチェロです。

16世紀から18世紀にかけて ヴァイオリンやチェロを製作した人は リュート 、シターン や テオルボ 、キタローネや ヴィオラ・ダ・ガンバ をよく知っている弦楽器製作者でした。

左側に1993年に ボローニャの博物館カタログとして出版された ” Strumenti Musicali Europei del Museo Civico Medievale di Bologna ” John Henry van der Meer の105ページに掲載してある、17世紀に製作されたと考えられる テオルボのヘッド写真を置きました。

両者とも、後ろから見たときに中心軸が右側に曲がっていくのが特徴となっています。左右の写真を見比べれば同じ軸取りがしてあるのが理解していただけると思います。

これらのことから、私はクレセント・カットなどのヘッド部の摩耗痕跡は人為的な加工 つまり、ヘッドの中央付近を上下に通る”ゆれるための軸”の調整痕跡であると判断しました。

 

 

Mandora 1420年頃 L 360.0 W 96.0 D 80.0( 83.0 ) / Wt. 255 g

ペグボックス壁部の厚さを左右差があるように製作すること自体は、ある意味では弦楽器製作者の常識でした。

“The Renaissance Cittern” Francis Palmer London 1617年

これは ルネサンス・シターンや テオルボ ( Theorbo ) などで、垂直軸に対して直交方向に取り付けられている ペグ、ナット、フレット、ブリッジなどの傾きや、ペグボックス部の左右壁厚差を見れば明白だと思います。

• 

• 

しかし 検証を進めた結果‥ 従来の宮廷音楽に加えて ヤコポ・ペーリ (1561-1633 ) や、クレモナに生まれ学び 後にヴェネツィアのサン・マルコ寺院楽長となった クラウディオ・モンテヴェルディ ( 1567-1643 ) 達が、1600年前後にオペラを誕生させたあたりから弦楽器には時代の風が吹いていたことが分りました。

オペラは 急速に普及し1637年には ヴェネツィアにサン･カッシアーノ劇場が開設されると歌劇場建設ブームが起こりました。この時期から 器楽や演奏会場の多様化は 急速に進んだようです。

たとえばフランスでは 1661年にルイ14世の親政が始まり ジャン＝バティスト・リュリ ( 1632-1687 )は 宮廷音楽監督に任命され、それまで以上に活躍しました。

Plan du Château de Versailles 1664年

1678年 (1678–1684 )                                                                                                The opulent Hall of Mirrors at the Palace of Versailles

また、アルカンジェロ・コレッリ ( 1653-1713 )は 1675年に ボローニャからローマに移り ヴァイオリン奏者として本格的な活動を始め、1679年にはカプラニカ劇場でオーケストラを指揮し、1681年にはトリオ・ソナタ 作品1 ( 全12曲 )を ローマで出版しています。

Arcangelo Corelli ( 1653-1713 )

Michelangelo’s design of New St. Peter’s Basilica

現在のローマにあるサン・ピエトロ大聖堂は 1506年に建設に着手し、ミケランジェロ ( Michelangelo Buonarroti 1475-1564 ) が 担当したドームは 1588年に着工し1593年に頂塔部の工事が終わりました。

そして1666年にやっと全体が竣工し完成しています。また、ヴェネツィア共和国では 1685年にアントニオ・ヴィヴァルディ( 1678-1741 ) がサン・マルコ大聖堂のヴァイオリニストに就任しています。

Guardi 1775年～77年「1763年の総督アルヴィセⅣモセニーゴの選出」

“サン・マルコ寺院” は 他の都市の中心的聖堂とは異なり、ヴェネツィア共和国時代はカトリック教会の司教座聖堂ではなく、公式には共和国総督の礼拝堂だったそうです。ですから 総督の館であるドゥカーレ宮殿と隣接し繋がっています。これはヴェネツィア共和国のカトリック教会からの政治的独立性の象徴とされ、このことにより宗教関連以外で使用されることも多かったようです。

“18世紀の音楽ホール事情”

これらの時代状況により、私は 1600年代中頃から 弦楽器は ペグボックスの上端位置などで左右差を強くすることも含めた基礎性能の改変がおこなわれたのではないか推測しています。

アンドレア・アマティに代表される黎明期の弦楽器より、17世紀中頃から アントニオ・ストラディヴァリ ( ca.1644-1737 )や、ヨーゼフ・ガルネリ ( “Guarneri del Gesù” 1698-1744 ) も含めた 多くの製作者の弦楽器で “動的”な要素が増やされていくのがこの証と言えるのではないでしょうか。